Equation of Time in astronomical clocks

Gerard Klijnsmit

(Thank you for the contribution, Gerard) 

The true Sun time, as can be seen on a Sundial, is not the same as mean clock
time. When the Sun is due south, then true Sun time at that location is 12 h noon
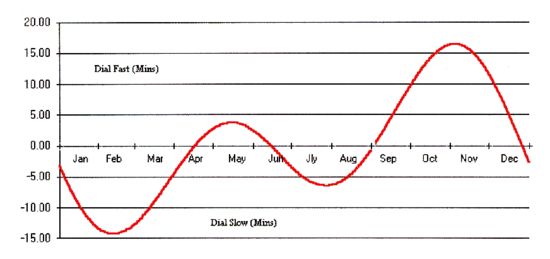
Our clocks will either be ahead or slower than 12 h at that same moment,
assuming no daylight saving time or location- longitude effects. Its maximum
deviation; where the true Sun is more than 16 minutes ahead is in early November
and the minimum deviation is around mid February when the Sun is 14 minutes
slower than the clock. This phenomenon is called the Equation of Time and it won't
change much in our daily routine, unless you are depending on knowing true Sun
time like navigators, using GPS etc.

Below a simplified time graph of the minute's deviation:

There are two reasons why this all is happening;

The first reason is the movement of the Sun along the ecliptic path. The Earth's
equator is tilted by 23.5 degrees to the path of the Sun; the ecliptic. The 23.5
degrees projection of the Suns motion onto the Earth's celestial equator, along
which "clock time" is measured, is at a maximum at the solstices; 21 June and
21 December, when the yearly movement of the Sun is almost parallel to the
equator,and is a minimum at the equinoxes 21 March and 21 September, when
the Sun moves in a sloping upward (March) or downward (September) direction.
It is the change in declination; the up/down move that leaves less for the parallel
component, which is the only component that affects the duration of the Solar day.
As a consequence of that, the daily shift of the shadow cast by the Sun in a
Sundial is smaller close to the equinoxes and greater close to the solstices

Schematic and very simplified look at this drawing:

 

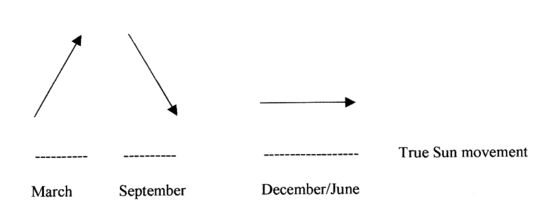
At the equinoxes, the Sun is seen slowing down by up to 20.3 seconds every
day and at the solstices speeding up by the same amount..

The second reason is the gravitational effect of the Earth's orbit, which is not a
perfect circle but slightly eccentric. The orbit of the Earth is an ellipse, and its
speed varies between 30.287 and 29.291 km/second. According to Kepler's laws
of planetary motion, the Sun then appears to move faster at perhelion, the point
Earth is closest to the Sun and slower in aphelion, the Earth furthest from Sun a
half year later. At these extreme points, the elliptical orbit effect increases
(respectively, decreases) the real Solar day by 7.9 seconds daily to a maximum
effect of 7.7 minutes. The zero points are reached at perhelion (at the beginning
of January) and aphelion (beginning of July) while the maximum values are in early
October (positive).

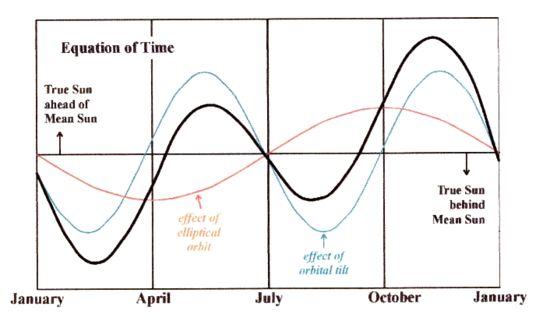
Both effects together will partly neutralize each other, while amplifying at other
moments during the year (November and February notably). The black line is the
EoT line of both effects together.
 

 To the main page